（文章最近发表在中国科学院智慧火花物理学栏目，标题：空间的维度）

目前为止，世界上没有一个理论说清楚四维和四维以上的空间几何架构的原理,数学家和物理学家都没有搞清楚。物理学最激动人心的玄理论就建立在多维空间上，如果不能正确解释多维空间，玄理论就没有出头之日。

                                                    一， 为什么会有不同维度的理解？

       1，由于相对论出现，爱因斯坦四维空间代替了牛顿的三维空间，四维是增加了一维时间，其实爱因斯坦对于空间依然是三维的长宽高。

       2，由于量子理论出现，出现了多维空间，有11维，除了一维时间外，空间是10维。不用说许许多多的一般人不知道多维空间是如何刻画的，就连物理学家数学家也没有说清楚，许许多多的人看了各种介绍多维空间的视频，仍然搞不清楚什么叫多维空间。因为在我们日常生活中仅仅是三维的长宽高。

      3，额外维是相对于“四维时空”而提出的一个概念，一般泛指的是理论在四维时空基础上扩展出来的其它维度。爱因斯坦提出宇宙是空间加时间组成的“四维时空”。

      1926年，德国数学物理学家西奥多卡扎鲁在四维时空上再添加一个空间维，也就是添加一个第五维，把爱因斯坦的相对论方程加以改写，改写后的方程可以把当时已知的两种基本力即“电磁力”和“引力”很自然地统一在同一个方程中。至此，理论中存在额外添加的维度统称为“额外维”。

     超弦理论中是一维时间十维空间或九维空间。

    4，在人所熟悉的三维空间里，有三对主要方向：上下（高度），南北（纬度），东西（经度）。这三对方向两两相交，也就是说，它们两两成直角。从数学方面讲，它们在三条不同的坐标轴 x、y、z上。

    5，纯空间性的四维空间另有一对垂直于其他三个主要方向的主要方向。这一对方向处在另一条同时垂直于x、y、z轴的坐标轴上，通常称作w轴。由于360度穷尽了二维，w轴如果需要存在，必然要重叠在三维之上。

                                                       二，维度是怎么得来的？
    1，  在算术加法中，个位满了就进一位到十位位置上。而空间维度增加却不是这样。
     2， 当数学家用圆把周围封闭起来的平面采用360度计量单位表示，再用一条直线穿过圆点就平分了圆，一个圆的一半就是180度，用90度垂直这条直线就可以刻画整个平面，平面坐标可以说清楚平面上的一切。高斯是第一个正确解释了二维图像坐标的数学家。

    3， 再从圆点发出一条垂直于平面的射线，形成了一个立体的三维坐标，经过圆点的无穷多个平面可以构成一个东西，我们叫做球。
三维空间可以穷尽我们可以观察到的整个空间。

     4，当我们看到一条直线，我们可以理解这条直线向周围扩展是三维的，庞加莱猜想就是基于三维空间，1904年，法国数学家亨利·庞加莱在提出了一个拓扑学的猜想:  任何一个单连通的，封闭的三维流形一定同胚于一个三维的球面。

三维空间坐标是由一个点发出的三条两两垂直的射线，他们有一个重要特征就是两两相连和互相垂直。

    5，皮耶罗将三维物体透视画法在二维平面上，但是，到了四维、五维、....高维是无法用透视法画出来的，高维的图像必须依赖霍奇猜想的方法——粘贴。

一个点状物体，在空间维度上没有延伸，因此空间维度为零，能够在三维空间自由移动；一根玄它有一个空间维度，能够在比自身有更多维度的空间移动。
       6，人们无法理解四维、五维、....、无穷多维的世界。因为360度平面正好是两个维度，不可能再插入一个维度，一个球体的中心只能发出三条两两相连互相垂直的射线，如果非要再增加一条射线，就会挤压原来的空间，坐标就不是90度的架构。

就连数学家和物理学家也没有办法说清楚。实际上数学家和物理学家也不清楚多维空间的几何本质是什么，他们也还在朦胧中纠结。

                                       三，下面就让我来告诉大家什么是三维以上的空间。

     1，三维空间基于两条重要原则：第一，三条射线两两相连互相垂直。第二，“同一维度不能重叠”。

因为圆点周围穷尽了整个空间，这是三维空间的基础，你在一个球上面加一个东西，说是球以外的，就没有意义，因为这个加上去的东西依然纳入球内。我们假设的球是一个开放的无穷边界的球。

记住欧氏几何与非欧几何都是【三维空间就是：1，由三条两两相连互相垂直的射线作为坐标。2，不能重叠。】

       2，现在关键的问题来了：如果我们构造四维空间，就必须放弃前面的一条规则，允许一个东西不是从圆心出发，并且与三维坐标的每一射线两两相连，互相垂直。允许这个东西必然与某一个维度重叠，于是，我们称之为第四维。

                                             四，下面我们将用图两说明。什么是四维空间呢？

      图1是一个平面，大家很容易理解，是二维的平面。

      图2是把平面卷起来对接成为一个管子，这个时候就不是平面了，是三维的，因为它有长宽高。最根本的特点就是：在一个三维空间，必然存在一个点，可以向两两垂直的方向发出射线。 

     图3是一个环面，依然是三维的。

    图4图5是两个环面连在一起，依然是三维，因为没有重叠。就是说它还只有一个点可以发出两两垂直的三条射线。

    图6依然是一个三维的,因为至少有一个方向无法重叠，例如我们俯瞰。

       五，四维空间是怎样形成的

  1，图7是一个环面，这是一个三维的结构，我们有假设一个点，用黑色圆圈表示，它可以向三个两两相连互相垂直的方向发出射线。

  2，图8是一个三叉管，它也是三维的，现在把图8三叉管安装在图7上，即图9，图9就是四维空间。图8的某一个射线与图7的射线可以垂直。

  3，  图10是射线的连接。出现了重叠，我们用一条紫色的粗线连接表示。，无论从哪一个方向都会有一个重叠的，这个就叫做四维空间。

4，四维空间就是有一个重叠。可以用四元数计算。

      关于直线，不是绝对的，例如我们从上海的海拔2米处发出一条射线到洛杉矶海拔2米处，由于地球的有弧度的，这一条直线只是俯瞰的直线，从地面看是弧线。

 六，多维空间是如何构造的

1，多维空间的构造思想是：用增加两两垂直的射线增加维度，重叠在三维空间外层，形成了多维空间。使得三维球外面的东西无法纳入三维球内，不得不用四维和更多维表示。

构造方法是著名的霍奇猜想的方法。参见科学智慧火花数学栏目：数学最重要的问题与物理学最重要的问题可以结合吗？

2，如果是五维空间，就是再加上四叉管(图中绿色的四叉管)，与其他区域两两相连，无论从哪一个方向都有两个重叠。

3，六维空间就是再加一个五叉管（黑色的五叉管），有三层重叠。

4，n维空间就是有n-3个重叠。以此类推，可以构造无穷多个维度的空间。10维空间图构造。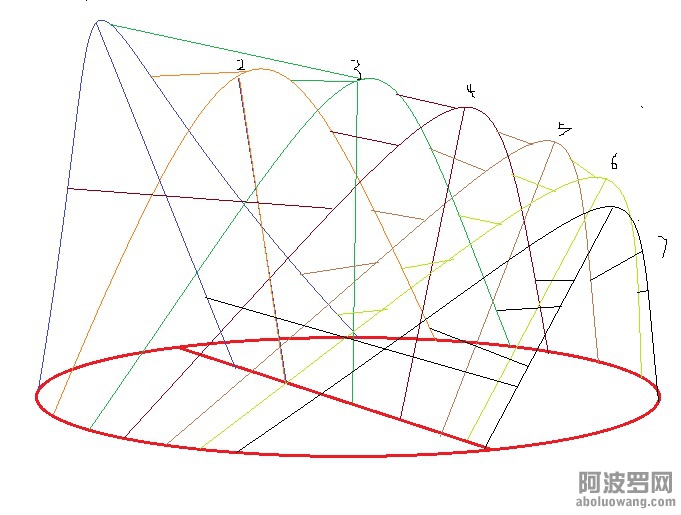物理学家想象的10维空间。

大家明白了没有？

5，在一个小范围的都是三维空间，再大一点的范围就是四维空间，再大就是五维空间，.....，如果宇宙是无穷大的，就有无穷多维空间。

一位物理学老师给学生讲26维空间的推导原理。

      我们从四色定理、曲面染色借助霍奇猜想到多维空间，如果把无穷多个两两互素的素数与无穷多个两两相连的区域一一对应，就把数论与图论与物理学联系起来。图9是一个岐管，岐管内是一个世界x，岐管外是一个世界y，，整个宇宙就是费马曲线，也就是费马大定理。管壁就是膜，我们把由量子力学进入弦理论——膜——膜宇宙。就是说宇宙的数学形式是有数学中最经典的问题组成。

黎曼几何为爱因斯坦相对论提供了几何框架；我们的多维架构为玄理论和M理论提供了架构。