|
哥德巴赫猜想也是一个初等数论问题 (转载于中国科学院智慧火花) 一,公式 公元前300年古希腊的埃拉托斯特尼创造了一种筛法,可以产生任意大的数以内的全部素数: 要得到不大于某个自然数 n 的所有素数,只要在2— n 中将不大于 素数的倍数全部划去即可。 素数的倍数全部划去即可。
上述筛法可以总结为: 1,如果 n 是合数,则它有一个因子d满足1 < d ≤ 。 。
2,若自然数n不能被不大于 任何素数整除,则n是一个素数。(【代数学词典】259页,上海教育出版社)。 任何素数整除,则n是一个素数。(【代数学词典】259页,上海教育出版社)。
可以把2的汉字内容等价转换成为英语字母公式:
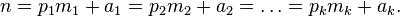 。.....(1) 。.....(1)
其中  表示前面的 k 个顺序素数2,3,5,....。 表示前面的 k 个顺序素数2,3,5,....。 ≠0。 ≠0。
这样解得的 n,若  ,,则n是一个素数。 ,,则n是一个素数。
我们可以把(1)式内容等价转换同余式组表示:
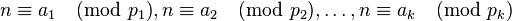 .........(2) .........(2)
由于(2)的模 , , ,..., ,..., 都是素数,因此两两互素,根据孙子定理(中国剩余定理)知,对于给定的 都是素数,因此两两互素,根据孙子定理(中国剩余定理)知,对于给定的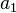 ,, ,, ,,...,, ,,...,, 。 。 (2)式在  ... ... 范围内有唯一解。 范围内有唯一解。
二,公式计算范例
例如:
k = 1 时, ,解得n=3,5,7。 ,解得n=3,5,7。
求得了(3, )区间的全部素数。 )区间的全部素数。
k = 2 时,(公式长度增加)  ,解得n=7,13,19; ,解得n=7,13,19;
 ,解得n=5,11,17,23。 ,解得n=5,11,17,23。
求得了(5, )区间的全部素数。 )区间的全部素数。
k=3时 | 
| 
| 
| 
|  | 31 | 7 和 37 | 13 和 43 | 19 |  | 11 和 41 | 17 和 47 | 23 | 29 |
求得了(7, )区间的全部素数。 )区间的全部素数。 仿此下去可以一个不漏地求得给定数以内的全部素数。
由孙子定理知,对于所有可能的 值,(1)和(2)式在 值,(1)和(2)式在  ... ... 范围内,有 范围内,有 ( )( )( )( )( )...( )...( )....(3)个解..。 )....(3)个解..。 (参考文献 1,【品数学】5页,清华大学出版社)吴振奎教授著

2,【关于一个寻找素数方法的理论依据】(中等数学杂志2001年4期)陈志云教授。
三,对称素数的合理框架
怎样使得两个自然数相加和相减都成为素数,即 N+X 成为素数,N-X 也是素数。
根据除法算式定理:“给定正整数a和b,b≠0,存在唯一整数q和r(0≤r<b),使a=bq+r”。
再根据同余定理:“每一整数恰与0,1,2,3,...,m-1中一数同余(mod m)”。、所以,任给一个自然数N(N>4),
都可以唯一表示成为:
 = = =...= =...= ....(4) ....(4)
其中, =0, 1,2, ,,...,, =0, 1,2, ,,...,, 。 。  , , ,,...,, ,,...,, .表示前面k个顺序素数2,3,5,....。 .表示前面k个顺序素数2,3,5,....。
 < N < < N < 
现在问,是否存在X,
 .....(5) .....(5)
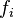 ≠ ≠ , ,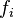 ≠ ≠ , ,
(5)式的同余形式:
 , , ,..., ,..., ....(6) ....(6)
如果X<N-2,则N+X与N-X都是素数,因为它们符合(1)(2)式。
四,对称素数计算范例:
设N=20,
 ; ;
 < 20 < < 20 < 
20的  ,; ,; ,; ,; .。 .。
四个解是:21,27,3,9。小于N-2的X有3和9,我们得知,20+3与20-3是一对素数;20+9与20-9是一对素数。 这就是利用素数判定法则:最小剩余不为零,并且 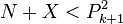 ,, 则N+X与N-X是一对素数。 ,, 则N+X与N-X是一对素数。
五,推论:
因为(N+X)+(N-X)=2N。这就是著名的哥德巴赫猜想猜想, 我们需要证明(5)式(6)式必然有小于 的解, 的解,
就证明了哥德巴赫猜想。孙子定理和埃拉托斯特尼筛法形成的公式已经为哥德巴赫猜想提供了合理框架,并且把问题转入到初等数论范围。 六,参考资料(【从台尔曼公式谈起】中等数学2002年5期)
|