|
|
哥德巴赫猜想的几何图形
摘要:哥德巴赫猜想几何模型是在埃拉特斯特尼筛法的基础上,借助霍奇猜想的方式完成的,成为一种可视化的东西。可以拍成视频教材。
一,我们首先利用霍奇猜想的粘贴方法(参见拙作:数学最重要的问题与物理最重要的问题可以结合吗,智慧火花数学栏目)。将下面的平面图中(区域1,2)上下对折,再左右对折形成一个环面,区域1表示第一个奇素数,区域2表示第二个奇素数,以此类推。再安上管子区域3,于是有3个区域两两相连,再继续安上三叉管,每一个管端与三个区域连接一起,于是有4个区域两两相连,一直继续进行下去,4叉是区域5,5叉是区域6,....。我们建立无穷多个两两相连区域。每一个区域都是代表一个奇素数,一 一 对应。
因为,素数最基本的特征就是:1,有无穷多个,2,所有的素数两两互素。与我们构造的几何图形1,有无穷多个区域,2,无穷多个区域两两相连。都是对应的。
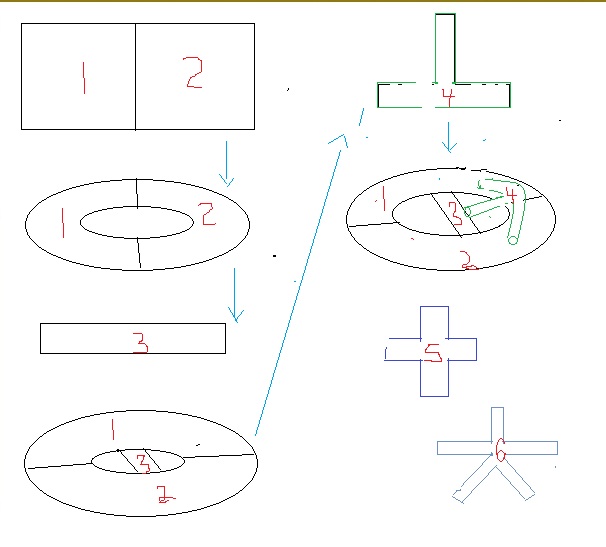
我们把上面的有无穷多个区域的素数网状架构倒过来,参见下面图,这个网状结构就是一个筛子。我们把大于6偶数当做被筛数灌入漏斗状的素数筛子:偶数8会在素数3(区域1)和素数5(区域2)结合处被拦截,就是不会被筛掉而从筛子漏掉到筛子外面。偶数10会在3和7结合部被拦截。一般认为,除了6必须是两个素数3之和,其他偶数都是不同的素数之和。
哥德巴赫猜想就是这个图:所有大于6的偶数都会被筛子拦截住,不会被遗漏到筛子外面。
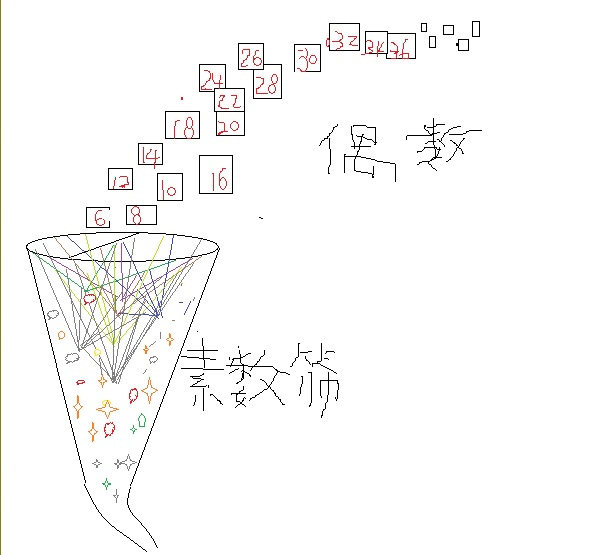
筛子就是:第一、素数的公式(参见智慧火花数学栏目,本人拙作:利用抽屉原理证明素数无穷多)
公元前300年古希腊的埃拉托斯特尼创造了一种筛法,可以产生任意大的数以内的全部素数: 要得到不大于某个自然数n的所有素数,只要在2—n中将不大于 素数的倍数全部划去即可。 素数的倍数全部划去即可。
上述筛法可以总结为
1,如果n是合数,则它有一个因子d满足1<d≤ 。 。
2,若自然数n是一个素数,当且仅当它不能被不大于 任何素数整除,则n是一个素数。)。 任何素数整除,则n是一个素数。)。
可以把2的汉字内容等价转换成为英语字母:
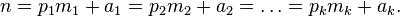 .........(1)  表示顺序素数2,3,5,....。 表示顺序素数2,3,5,....。 ≠0。 ≠0。
这样解得的n,若 ,则n是一个素数。 ,则n是一个素数。
我们可以把(1)式内容等价转换同余式组表示:
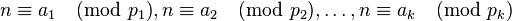 ..........(2)  , , ,..., ,..., 都是素数,因此两两互素,根据孙子定理(中国剩余定理)知,对于给定的 都是素数,因此两两互素,根据孙子定理(中国剩余定理)知,对于给定的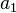 , , ,..., ,..., ,(2)式在 ,(2)式在  ... ... 范围内有唯一解。 范围内有唯一解。
范例
例如: k=1时, ,解得n=3,5,7。求得了(3, ,解得n=3,5,7。求得了(3, )区间的全部素数。 )区间的全部素数。
k=2时, ,解得n=7,13,19; ,解得n=7,13,19; ,解得n=5,11,17,23。求得了(5, ,解得n=5,11,17,23。求得了(5, )区间的全部素数。 )区间的全部素数。
k=3时
| 
| 
| 
| 
|  | 31 | 7,37 | 13,43 | 19 |  | 11,41 | 17,47 | 23 | 29 |
求得了(7, )区间的全部素数。 仿此下去可以一个不漏地求的任何给定数以内的全部素数。由孙子定理知,对于所有可能的 )区间的全部素数。 仿此下去可以一个不漏地求的任何给定数以内的全部素数。由孙子定理知,对于所有可能的 值,(1)和(2)式在 值,(1)和(2)式在  ... ... 范围内,有 范围内,有
( )( )( )( )( )...( )...( )....(3)个解。 )....(3)个解。
.
偶数倒入筛子的过程就是:第二部分,对称素数的合理框架
(一)怎样使得两个自然数相加和相减都成为素数,即N+X成为素数,N-X也是素数。
根据除法算式定理:“给定正整数a和b,b≠0,存在唯一整数q和r(0≤r<b),使a=bq+r”。
再根据同余定理:“每一整数恰与0,1,2,3,...,m-1中一数同余(mod m)”。
所以,任给一个自然数N (N > 4 ),都可以唯一表示成为:
 = = =...= =...= ....(4) ....(4)
其中, =0, 1,2, ..., =0, 1,2, ..., 。 。
 , , ,,...,, ,,...,, .表示前面k个顺序素数2,3,5,....。 .表示前面k个顺序素数2,3,5,....。
 < N < < N < 
现在问,是否存在X,
 .....(5) .....(5)
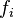 ≠ ≠ , ,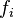 ≠ ≠ , ,
(5)式的同余形式:
 , , ,..., ,..., ....(6) ....(6)
如果X<N-2,则N+X与N-X都是素数,因为它们符合正文中的(1)(2)式。
(二)对称素数计算范例:
设N=20,
 ; ;
 < 20 < < 20 <
 ,; ,; ,; ,; .。 .。
构造x
| 
| 
| 
| 
|  | 21 | 27 | 3 | 9 | 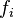 ≠ ≠ , ,
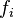 ≠ ≠ , ,
|  , ,
 , ,
 . . |  , ,
 , ,
 . . |  , ,
 , ,
 . . |  , ,
 , ,
 . . |
四个解是:21,27,3,9。小于N-2的X有3和9,我们得知,20+3与20-3是一对素数;20+9与20-9是一对素数。 这就是利用素数判定法则:最小剩余不为零,并且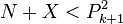 ,,则N+X与N-X是一对素数。 ,,则N+X与N-X是一对素数。
(三)推论:因为(N+X)+(N-X)=2N。这就是著名的哥德巴赫猜想猜想, 我们需要证明(5)式(6)式必然有小于 的解,就证明了哥德巴赫猜想。孙子定理和埃拉托斯特尼筛法形成的公式已经为哥德巴赫猜想提供了合理框架,并且把问题转入到初等数论范围。 的解,就证明了哥德巴赫猜想。孙子定理和埃拉托斯特尼筛法形成的公式已经为哥德巴赫猜想提供了合理框架,并且把问题转入到初等数论范围。
(四)上面内容参见:参考资料(【从台尔曼公式谈起】中等数学2002年5期)http://wenku.baidu.com/view/b97bb865915f804d2a16c102.html
现在,我们有了哥德巴赫猜想的公式模型和几何模型。因此,更加清晰明了。
日本的数学教学有很多视频,夸张性的教学很适应学生。但是,数论中的教学不容易理解,特别是黎曼猜想和费马大定理。
|
|