华罗庚证明华林猜想纯属无稽之谈

wxmwrk

    有人说华罗庚证明了华林猜想，纯属无稽之谈，1770年，华林发表了《代数沉思录》（Meditationes Algebraicae），其中说，每一个正整数至多是9个立方数之和；至多是19个四次方之和。还猜想，每一个正整数都是可以表示成为至多r个k次幂之和，其中r依赖于k。

      

王元说：“华罗庚证明了：假定fi(x)(1<=i<=s)为满足必须满足的条件的k次整值多项式。则当s>=2k+1时，方程：

N=f1(x1)+…+fs(xs)   的解数有一个渐近公式。特别对于华林问题，即方程：

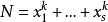，当s>=2k+1时，对充分大的N，有非寻常非负解，且解数有渐近公式。”   

  

    知道华罗庚哪里错误吗？华罗庚的推理建立在预期理由的错误前提下：

1，假定。

假定，只能用在否定结果的证明中，例如，欧几里得证明素数无穷多个。

（1），假定a成立，可以推出b，得到c，c与a矛盾，所以假定的a不能成立，得到非a）。

（2），不能用在肯定的结论（假定a，可以推出b，得到c，c=a，或者c包含a，所以假定的a成立，这个就是预期理由的错误）。

2，充分大。（充分大是一个错误概念，一个正确的数学概念必须具备专一性，精确性，稳定性，可以检验性）。

以华罗庚和王元这种垃圾水平数学家，怎么会懂得数学证明？