A德摩根实际上已经证明了四色定理

wxmwrk

摘要：

1，德摩根企图证明四色定理，他证明了平面地图染色当且仅当无法构造需要5种颜色的 5 个两两相连的区域，4种颜色就够了，若p则q。

（暗含如果证明不能构造需要4种颜色染色的4个两两相连区域，那么，3种颜色就够了，若p’则q’。但是，这个暗含的“漏洞”无法发生在2维平面上，因为，我们可以在平面是构造一个有4个两两相连区域，见图一）。

2，否定德摩根的理由是一种间接类比反驳，反驳的不是德摩根正面的理由，若p则q。

而是反驳并不存在的暗含的漏洞：若p’则q’，图二在平面上可以没有4个两两相连区域，依然需要4种颜色，3种颜色不够。非p’则非q’。

3，类比反驳成功的标志是，构造与对方论题或者论据相矛盾的正确例子，以表明两种事物不能同真。如果要成功否定德摩根的理论，只有一条标准，就是：构造一个不用5个区域两两相连的图形，依然需要5种颜色染色。而不是攻击根本就不存在的假定。

关键词：颜色；区域；两两相连

一，Augustus De Morgan 的想法

第1，平面或者球面染色需要4种颜色，并且轻而易举构造了4个区域两两相连。

A 德摩根是对四色定理理论有贡献的第一人。他是伦敦大学的教授（1806-1871），图一是说平面上 4 个区域需要 4 种颜色，因为图一是4个区域两两相连，等价于需要4种颜色才能区别4个区域。

第2，证明了平面上不能存在五个区域两两相连（当时的话叫做：5个国家不能每一个都和其余相邻）。下面是 A 德摩根的证明，不能在平面上构造一个有5个两两相连区域（供参考）：

二，反驳者的理由

下面的图二是反驳者推翻 A 德摩根四色定理不一定能成立的逻辑：

图二是在图一的基础上加入两个区域，图二的 6 个国家（区域）中 A，B，C，D，E，F 没有哪 4 个是两两相连的，然而仍需要 4 种颜色（数字代表颜色编号），外围的需要 3 种，中间的需要 4 种。

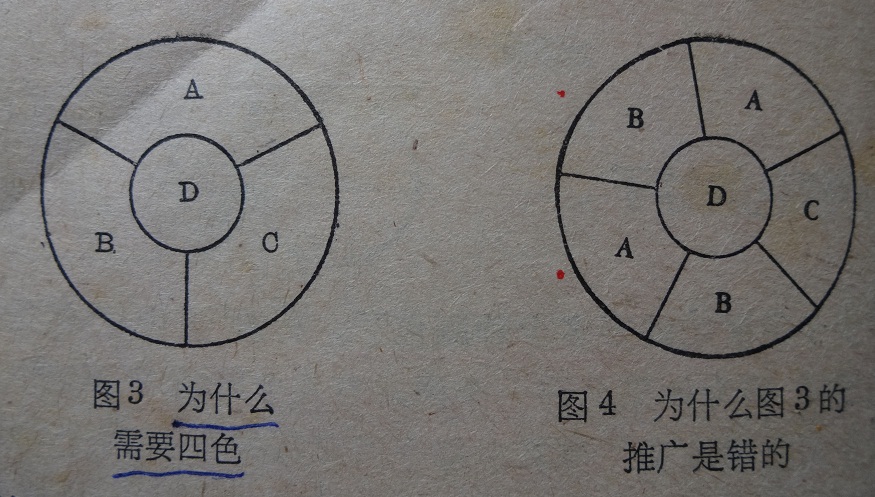
三，为什么否定德摩根的理由不能成立

首先，反驳者没有从属性上推翻需要4种颜色。图一表明平面需要4种颜色。反驳者的图二也是肯定需要4种颜色。就是说，反驳者与肯定者是一致的。

其次，反驳者没有通过类比方法否定德摩根的“当且仅当可以构造5个两两相连区域，则需要5种颜色”

而是去否定一个不存在的暗含的理由“如果不能构造需要4种颜色染色的4个两两相连区域，那么，3种颜色就够了”但是暗含的理由是根本不存在的。不能否定一个不存在的东西。因为，世界上根本无法在小于2维的几何上去构造一个：有3个两两相连区域，而不能构造4个两两相连区域。

可以肯定说，德摩根已经证明了四色定理。他被误解了 150 年。

参考文献：【今日数学】第二部分，四色问题。K阿佩尔；w黑肯